- ╚źç°Ży(tĘ»ng)Ď╗ńN╩█čßżÇú║
- ▒▒żę┐é▓┐ú║
- 010-64437473
- ╔¤║úú║
- 021-62113795
- ╔ţ█┌ú║
- 0755-86241216
Ş▀ë║╦«╔ń┴¸ë║┴ŽßîĚ┼đžĹ¬(yĘęng)Á─└ÝŇôĚÍ╬÷║═ë║┴ŽËő(jĘČ)╦Ń
Ľr(shʬ)Úgú║2012-11-29 üÝď┤ú║ http://m.tadokuzemi.com
đÂŢd║═╝ËŢdĎ╗śË┐╔Ďď╩╣╩▄Ţd╬´┴¤░l(fĘí)╔˙ĂĂë─íú═ČśËúČţw┴úď┌Ď║ˇwÁ─ýo╦«ë║┴ŽÎ¸Ë├¤┬úČË╔Ë┌ĆŚđďÎâđ╬°ˇwĚe┐sđíúČ▓óď┌ţw┴úÍđâŽ(chĘ│)┤ŠĆŚđďŬ(yĘęng)Îâ─▄íú«ö(dĘíng)ë║┴Ž═╗╚╗ßîĚ┼Ľr(shʬ)úČâŽ(chĘ│)┤Šď┌ţw┴úÍđÁ─Ŭ(yĘęng)Îâ─▄Ľ■(huĘČ)ŰSÍ«ßîĚ┼íúË╔Ë┌▓─┴¤Á─┐╣└şĆŐ(qiĘóng)Â╚▀h(yuĘún)▀h(yuĘún)Á═Ë┌Ăń┐╣ë║ĆŐ(qiĘóng)Â╚úČ°ăĎŬ(yĘęng)Îâ─▄Á─═╗╚╗ßîĚ┼║═ĹTđďθË├ż═Ľ■(huĘČ)îž(dĘúo)Í┬ţw┴úđÂŢdĽr(shʬ)Á─└şĹ¬(yĘęng)┴ŽĂĂë─íú
ď┌Ş▀ë║╦«╔ń┴¸Ě█╦ÚÍđúČ╬´┴¤ţw┴ú▒╗╝Ë╚ŰÁŻ╦«╔ń┴¸ÍđúČ╩Τ╚ţw┴ú╩▄ÁŻýo╦«ë║┴Ž▒╗╝Ëë║ÁŻŞ▀ë║áţĹB(tĘĄi)úČ╩╣Á├ţw┴úâ╚(nĘĘi)âŽ(chĘ│)┤ŠËđ║▄Ş▀Á─ĆŚđďŬ(yĘęng)Îâ─▄úČ╚╗║ˇŻŤ(jĘęng)╦«╔ń┴¸╝Ë╦┘°▒╗═╗╚╗ßîĚ┼úČîŹ(shʬ)ČF(xiĘĄn)ë║┴ŽßîĚ┼đžĹ¬(yĘęng)°▒╗Ě█╦Úíú
îŽË┌═╗╚╗đÂŢdÁ─Ţd║╔ßîĚ┼đžĹ¬(yĘęng)úČ╬Ďéâ┐╔Ďď═Ę▀^║ćć╬Á─ĆŚ╗╔╝ËđÂŢd▀^│╠üÝŇf├¸íú
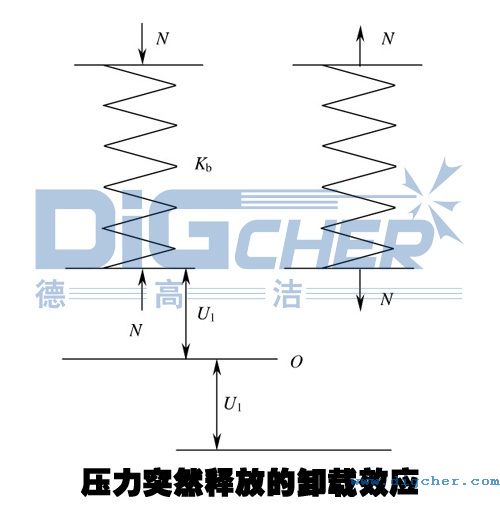
╔¤łD╦¨╩żÁ─ĆŚ╗╔úČĂńäéÂ╚×Ú 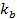 úČ«ö(dĘíng)θË├ď┌Ăń╔¤Á─┴Žď÷┤ˇÁŻ N Ľr(shʬ)úČĆŚ╗╔Â╦▓┐▒╗ë║┐sÁŻ
úČ«ö(dĘíng)θË├ď┌Ăń╔¤Á─┴Žď÷┤ˇÁŻ N Ľr(shʬ)úČĆŚ╗╔Â╦▓┐▒╗ë║┐sÁŻ  úČ°¤ÓŬ(yĘęng)ĆŚ╗╔Á─ë║┐sŬ(yĘęng)Îâ─▄×Ú
úČ°¤ÓŬ(yĘęng)ĆŚ╗╔Á─ë║┐sŬ(yĘęng)Îâ─▄×Ú 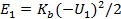 íú┤╦Ľr(shʬ)╚š╣űîóθË├┴Ž N ═╗╚╗ĎĂ╚ąúČĆŚ╗╔┴ó╝┤¤┬ĆŚúČ▓ó░l(fĘí)╔˙Ň˝äË(dĘ░ng)íúË╔Ë┌─▄┴┐╩ě║ŃúČĂń¤┬Â╦╦▓ÚgÎţ┤ˇ╬╗ĎĂ┐╔▀_(dĘó)ĂŻ║Ô╬╗Í├ O Řc(diĘún)Ďď¤┬Á─
íú┤╦Ľr(shʬ)╚š╣űîóθË├┴Ž N ═╗╚╗ĎĂ╚ąúČĆŚ╗╔┴ó╝┤¤┬ĆŚúČ▓ó░l(fĘí)╔˙Ň˝äË(dĘ░ng)íúË╔Ë┌─▄┴┐╩ě║ŃúČĂń¤┬Â╦╦▓ÚgÎţ┤ˇ╬╗ĎĂ┐╔▀_(dĘó)ĂŻ║Ô╬╗Í├ O Řc(diĘún)Ďď¤┬Á─  ╠ÄíúĎ▓ż═╩ăŇf═╗╚╗đÂŢdÁ─Ţd║╔đžĹ¬(yĘęng)úȤӫö(dĘíng)Ë┌îó┴┐ÍÁ¤Ó═ČÁ─║╔ŢdúČĚ┤¤˛╝ËÁŻĂń╔¤íú
╠ÄíúĎ▓ż═╩ăŇf═╗╚╗đÂŢdÁ─Ţd║╔đžĹ¬(yĘęng)úȤӫö(dĘíng)Ë┌îó┴┐ÍÁ¤Ó═ČÁ─║╔ŢdúČĚ┤¤˛╝ËÁŻĂń╔¤íú
┼cďş╝ËŢd▓╗═ČÁ─╩ăúČ╝ËŢdĽr(shʬ)ĆŚ╗╔│đ╩▄Á─╩ăë║Ŭ(yĘęng)┴ŽúČ°đÂŢdĽr(shʬ)ĆŚ╗╔│đ╩▄Á─╩ă└şĹ¬(yĘęng)┴ŽíúîŽË┌┐╣└şĆŐ(qiĘóng)Â╚Á═Ë┌Ăń┐╣ë║ĆŐ(qiĘóng)Â╚Á─▓─┴¤úČ▓╔Ë├ë║┴ŽßîĚ┼▀M(jĘČn)đđĚ█╦Ú╩ă═ŕ╚ź┐╔đđÁ─íúîŹ(shʬ)ŰH╔¤úČ┤ˇÂÓöÁ(shĘ┤)┤Óđď▓─┴¤Â╝ż▀Ëđ┐╣└şĆŐ(qiĘóng)Â╚▀h(yuĘún)▀h(yuĘún)Á═Ë┌Ăń┐╣ë║ĆŐ(qiĘóng)Â╚Á─╠ěđďíú
ިô■(jĘ┤)öÓ┴Đ┴ŽîW(xuĘŽ)┐╔ͬúČ╣╠ˇwţw┴úď┌═Ô┴ŽÎ¸Ë├¤┬úČĂńĆŚđďŬ(yĘęng)Îâ─▄▓╗öÓď÷╝ËúČ▀_(dĘó)ÁŻĎ╗ÂĘ│╠Â╚║ˇúČż═ď┌ţw┴úâ╚(nĘĘi)đ╬│╔┴Đ╝y╗˛╩╣┴Đ╝y▓╗öÓöU(kuĘ░)Ň╣úČ▀M(jĘČn)°╩žĚÇ(wĘžn)ĂĂ┴ĐíúĂń┴Đ╝y«a(chĘún)╔˙║═öU(kuĘ░)Ň╣Á──▄┴┐╚ź▓┐üÝÎďË┌ţw┴úâ╚(nĘĘi)âŽ(chĘ│)┤ŠÁ─ĆŚđďŬ(yĘęng)Îâ─▄íú
╝┘ďO(shĘĘ)▒╗Ě█╦ÚÁ─╬´┴¤ţw┴ú×ÚŞ¸¤˛═Čđ│ä˛ă˛úČă˛Á─░ŰĆŻ×Ú búČď┌ă˛═Ô▒Ý├Š╩▄ż¨ä˛ë║┴Ž p Á─θË├íúË╔ă˛?qĘ▒)ŽĚQćľţ}Á─ĂŻ║Ô╬óĚÍĚŻ│╠ú║
┐╔ĎďŻÔÁ├ţw┴ú╩▄ÁŻÁ─Ŭ(yĘęng)┴Ž▒Ý▀_(dĘó)╩Ż×Úú║
ď┌ë║┴ŽÎ¸Ë├¤┬Á─Ŭ(yĘęng)Îâ?yĘşu)Úú?/div>
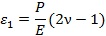 ╣ź╩Ż(3)
╣ź╩Ż(3)
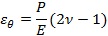 ╣ź╩Ż(4)
╣ź╩Ż(4)
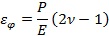 ╣ź╩Ż(5)
╣ź╩Ż(5)
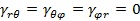 ╣ź╩Ż(6)
╣ź╩Ż(6)
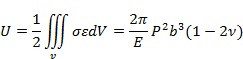 ╣ź╩Ż(7)
╣ź╩Ż(7)
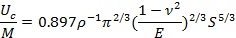 ╣ź╩Ż(8)
╣ź╩Ż(8)
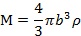 ╣ź╩Ż(9)
╣ź╩Ż(9)
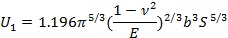 ╣ź╩Ż(10)
╣ź╩Ż(10)
ätţw┴úď┌ë║┴Ž p θË├¤┬Á─Ŭ(yĘęng)Îâ─▄×Úú║
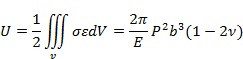 ╣ź╩Ż(7)
╣ź╩Ż(7)ިô■(jĘ┤)ĂĂ╦Ú┴ŽîW(xuĘŽ)Đđż┐│Č╝Ü(xĘČ)─ąÁVĽr(shʬ)úČîóĂĂ╦Ú─▄ÂĘ┴x×Úú║Ţö╚ŰÁŻă˛đ╬ţw┴ú╔¤▀_(dĘó)ÁŻ╦▓Ľr(shʬ)ĂĂ╦ÚÁ─ĆŚđďŬ(yĘęng)Îâ─▄íú▓ó═Ăîž(dĘúo)Á├│÷ć╬╬╗┘|(zhĘČ)┴┐ĂĂ╦Ú─▄┼cĆŐ(qiĘóng)Â╚Á─ŕP(guĘín)¤Á×Úú║
îŽË┌░ŰĆŻ×Ú b Á─ă˛đ╬ţw┴úú║
┤˙╚Ű╣ź╩Ż(8)┐╔Á├ú║
«ö(dĘíng)ţw┴ú╩▄ÁŻż¨ä˛ë║┴Ž p ║ˇúČď┌Ăńˇwâ╚(nĘĘi)ĎĐż█╝»┴╦╚š╣ź╩Ż(7)╦¨╩żÁ─ĆŚđďŬ(yĘęng)Îâ─▄íú╚š╣űîóż¨ä˛ë║┴Ž p ═╗╚╗ßîĚ┼úČät㲡wâ╚(nĘĘi)îó│÷ČF(xiĘĄn)└ş╔ýŬ(yĘęng)┴Žíúϲ┤╦úČţw┴ú╦¨╩▄Á─Ŭ(yĘęng)┴ŽÍ╗Ϭ▀_(dĘó)ÁŻ▓─┴¤Á─└ş╔ýĆŐ(qiĘóng)Â╚ż═Ľ■(huĘČ)▒╗ĂĂë─íú╦¨ĎďúČ╣ź╩Ż(10)Á─ĆŐ(qiĘóng)Â╚ S ż═┐╔Ë├▓─┴¤Á─└ş╔ýĆŐ(qiĘóng)Â╚ σl üÝ┤˙╠ŠúČät╣ź╩Ż(10)┐╔Îâ?yĘşu)Úú?/div>
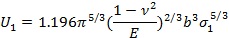 ╣ź╩Ż(11)
╣ź╩Ż(11)
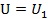 ╣ź╩Ż(12)
╣ź╩Ż(12)
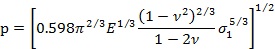 ╣ź╩Ż(12)
╣ź╩Ż(12)
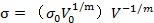 ╣ź╩Ż(13)
╣ź╩Ż(13)
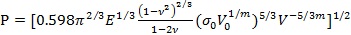 ╣ź╩Ż(14)
╣ź╩Ż(14)
ďO(shĘĘ)Ěeż█ď┌ţw┴úâ╚(nĘĘi)Á─ĆŚđďÎâđ╬─▄úČď┌ßîĚ┼Ľr(shʬ)╚ź▓┐ŮD(zhuĘún)Îâ?yĘşu)Úţw┴úÁ─ĂĂ╦Ú─▄ú║
╝┤ú║
╣ź╩Ż(12)Ňf├¸ţw┴úď┌ë║┴Ž═╗╚╗ßîĚ┼Ľr(shʬ)Á├ÁŻĂĂë─úČđŔŻoËŔă˛đ╬ţw┴úÁ─ż¨ä˛ë║┴Ž p Á─▒Ý▀_(dĘó)╩Żíú
╚š╣ű┐╝Ĺ]ĆŐ(qiĘóng)Â╚ŰSˇwĚeÁ─ÎâôQúČätŻo│÷Á─ĆŐ(qiĘóng)Â╚ŕP(guĘín)¤Á×Úú║
╝┤ú║
╔¤╩ŻÍđúČ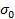 —ć╬╬╗ˇwĚeďçśË
—ć╬╬╗ˇwĚeďçśË 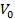 Á─└ş╔ýĆŐ(qiĘóng)Â╚ú╗
Á─└ş╔ýĆŐ(qiĘóng)Â╚ú╗
m —▓─┴¤Á─ż¨ä˛đď¤ÁöÁ(shĘ┤)íú
╣ź╩Ż(14)▒Ý├¸úČϬ╩╣░ŰĆŻ×Ú b Á─ă˛đ╬ţw┴ú╩▄ë║ßîĚ┼Ě█╦Ú╦¨đŔÁ─ë║┴ŽúČÍ╗┼cţw┴ú▓─┴¤Á─╬´└Ý┴ŽîW(xuĘŽ)╠ěđď║═ÄÎ║╬│▀┤šËđŕP(guĘín)íú
Ë╔┤╦┐╔ͬúČ═Ę▀^ë║┴ŽßîĚ┼Ě█╦Ú╬´└Ý╦¨đŔÁ─ë║┴Ž▒╚▓─┴¤Á─┐╣└şĆŐ(qiĘóng)Â╚Ş▀úČÁźĎ¬▒╚▓─┴¤Á─┐╣ë║ĆŐ(qiĘóng)Â╚Á═║▄ÂÓíú═ČĽr(shʬ)úČθË├ď┌ţw┴ú╔¤Á─ż¨ä˛ë║┴ŽďŻ┤ˇúČĚeż█ď┌ţw┴úâ╚(nĘĘi)Á─ĆŚđďŬ(yĘęng)Îâ─▄ż═ﯪ▀úČë║┴ŽßîĚ┼║ˇÁ─Ě█╦Úđž╣űż═ďŻ║├íú
- ś╦(biĘío)║×ú║
- └ÝŇôĚÍ╬÷
- ë║┴ŽËő(jĘČ)╦Ń
- Ş▀ë║╦«╔ń┴¸
- ë║┴ŽßîĚ┼đžĹ¬(yĘęng)
Ëđđž╠ߪ▀çŐÎýë█├ŘÁ─ÄÎéÇ(gĘĘ)ĚŻĚĘ
2017-08-14
Ş▀ë║ăň¤┤ÖC(jĘę)ăň¤┤ÖC(jĘę)└ÝĚÍ╬÷Í«Îţ┤ˇăň¤┤îĺÂ╚Á─
2012-09-18
Ş▀ë║╦«╔ń┴¸Îţ┤ˇ┤˛ô˘┴ŽîŹ(shʬ)ťy
2013-05-03
Ş▀ë║ăň¤┤ÖC(jĘę)▀M(jĘČn)╦«ă╗├▄ĚÔ╩žđžÁ─ďşĎ˛ĚÍ╬÷
2013-06-29
Ş▀ë║ăň¤┤ÖC(jĘę)Ş▀ë║─z╣▄Â╬ë║┴Žôp╩ž└ÝŇôĚÍ╬÷
2012-07-06



